When it comes to Marketing Mix Modeling (MMM), the goal is simple: identify how different marketing channels, such as TV, digital ads, and promotions, influence key business outcomes like sales or brand awareness. However, the reality of building these models can be complex, especially when using traditional statistical approaches like multiple linear regression and Maximum Likelihood Estimation (MLE).
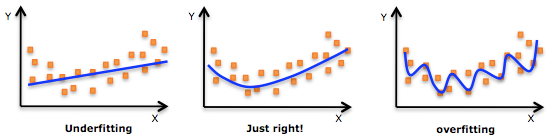
One common pitfall in traditional MMM is overfitting. Overfitting occurs when a model becomes too finely tuned to the historical data, learning patterns that may not generalize to new data. This can result in models that appear accurate on paper but fail to provide reliable insights when it comes to making real-world decisions. Let’s explore how Bayesian statistics, with its ability to incorporate priors, helps overcome these challenges and leads to more robust and actionable models.
Multiple Linear Regression and Maximum Likelihood Estimation (MLE)
At the heart of most traditional MMM approaches lies multiple linear regression. This method attempts to establish a relationship between different independent variables (such as media spend on various channels) and a dependent variable (like sales). The model tries to determine how much each media channel contributes to the overall outcome by estimating a set of weights for the variables.
This estimation is typically done using Maximum Likelihood Estimation (MLE). MLE works by finding the set of parameters that make the observed data most likely under the model’s assumptions. While MLE is a powerful method, it has its limitations when it comes to sparse or noisy data common issues in marketing. This can lead to overfitting, especially when there are many variables (media channels) and fewer time periods (data points) to train the model on.
For example, if you run TV ads infrequently, the model might over-attribute spikes in sales to other factors, or worse, overestimate the importance of channels that aren’t contributing as much, simply because the data is sparse.
The Pitfall of Overfitting
Overfitting happens when a model becomes too complex and starts “fitting” the noise in the data rather than the true underlying patterns. In MMM, this is particularly problematic when you have limited data or when certain channels (like TV or outdoor advertising) are only used occasionally. The model might pick up random fluctuations in sales and attribute them to those channels, resulting in misleading insights.
In a situation where overfitting occurs, your model may suggest that a certain media channel is highly effective, when in reality, it’s picking up on random variations in the data. This could lead to poor decision-making, where resources are allocated to ineffective media channels based on incorrect model insights.
Bayesian Statistics is Key to Beating Overfitting
This is where Bayesian statistics comes in. Unlike traditional regression methods, Bayesian statistics doesn’t just rely on the observed data it allows you to include prior knowledge about how media channels and marketing activities should behave.
Bayesian modeling avoids overfitting by introducing regularization, which essentially penalizes extreme or unlikely parameter estimates. By incorporating prior assumptions about how certain variables should behave Bayesian MMM can guide the model toward more reasonable outcomes, even when data is limited or noisy.
How Priors Encode Domain Knowledge in Bayesian Marketing Mix Models
One of the most powerful tools in Bayesian statistics is the ability to encode domain knowledge through priors. Priors are essentially assumptions that reflect your understanding of how different media channels or marketing activities work in the real world. These priors act as guardrails, helping the model stay grounded in reality.
For example, consider TV advertising. You might know that the impact of a TV ad is unlikely to occur entirely on the day it airs there’s a carryover effect that lasts for several days, weeks or even months. You can encode this knowledge as a prior, guiding the model to expect that TV ads will have a delayed and gradually diminishing effect on sales, rather than a sharp spike on the day the ad runs.
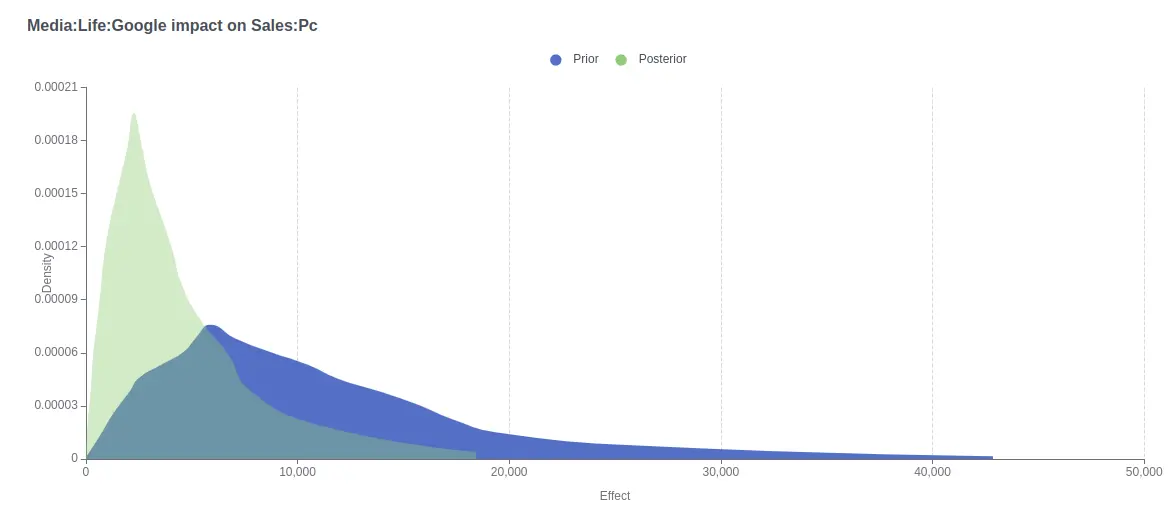
Similarly, you might have prior knowledge that certain marketing channels, such as print or radio, typically have a positive return on investment (ROI), but the ROI is likely to be below a certain threshold. By setting priors that reflect this, the model is less likely to overestimate the effectiveness of those channels when data is sparse.
The Benefits of Uncertainty Quantification
One of the key advantages of Bayesian statistics is that it doesn’t just provide point estimates for parameters it provides a posterior distribution. This means that instead of just telling you what the most likely impact of a media channel is, the model gives you a range of possible outcomes and quantifies the uncertainty associated with those estimates.
For instance, if you’ve only run TV ads for a few weeks, the model will recognize that it doesn’t have enough data to be highly confident in its predictions for TV. On the other hand, if you’ve been running digital ads continuously for months, the model will be much more confident in the ROI estimates for digital channels.
This uncertainty quantification is crucial for risk-aware decision-making. If the model tells you there’s a wide range of possible outcomes for TV ads, you might decide to allocate budget cautiously, knowing that the results are uncertain. Conversely, if the model is highly confident about the impact of digital ads, you can allocate more budget with confidence that the expected returns will materialize.
Why Choosing the Right Priors Is Critical
The choice of priors in a Bayesian MMM isn’t just about preventing overfitting it’s about making the model more reflective of real-world marketing dynamics. Priors can be used to:
- Set realistic expectations: By encoding reasonable expectations about media performance, you ensure that your model doesn’t get swayed by short-term fluctuations or limited data.
- Optimize budget allocation: With priors in place, your model provides more accurate estimates of the true ROI of each channel, enabling better budget allocation.
- Reflect real-world media behavior: Priors allow you to account for real-world phenomena like delayed effects (carryover) from media channels. For example, TV ads might have an impact that lasts days or even weeks after the ad airs, and priors help incorporate this into the model.
By setting appropriate priors, you guide the model to more meaningful insights and predictions, ensuring that your marketing investments are both data-driven and grounded in reality.
Bayesian MMM for More Reliable Decision-Making
Traditional multiple linear regression models using MLE can struggle with overfitting, especially when data is sparse or noisy. Bayesian statistics offers a powerful alternative by allowing you to incorporate priors your domain knowledge into the model, improving both the accuracy and reliability of the results.
With Bayesian modeling, you also gain the advantage of uncertainty quantification, which enables you to make risk-aware decisions about how to allocate your marketing budget. Rather than relying solely on point estimates, you can see the range of possible outcomes and choose the most appropriate strategy based on your risk tolerance.
Incorporating Bayesian hierarchical modeling into MMM isn’t just about overcoming the limitations of traditional methods. It’s about building models that truly reflect the complexity of the real world, allowing you to make smarter, more informed marketing decisions.